|
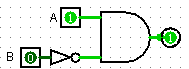
Tendo em conta a expressão X Ver Exemplo a) Calcular o nº de saídas possíveis b) Desenhar o circuito no logisim c) Desenhar o diagrama temporal d) Preencher a tabela de verdade e) Conclusão |
||||||||||||
|
|
|
06-11-2017 |
08-11-2017 |
10-11-2017 |
10-11-2017 |
13-11-2017 |
|
15-11-2017 |
|
20-11-2017 |
|
|
|
|
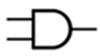
Porta AND
|
A.B.C |
A. |
A.B. (No logisim
resolve o exercício utilizando portas de 3 entradas e utilizando portas de
apenas 2 entradas) |
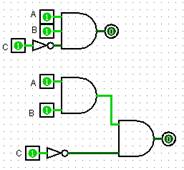
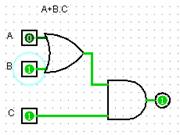
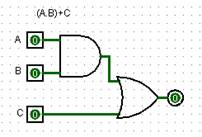
Desafio3.1AndOr (A+B).C Desafio3.2OrAnd (A.B)+C Desafio3.3AndOrNot
( Desafio A - Agrupa todas as expressões numa só tabela e compara os valores pondo-os em evidência na tabela de verdade. Resolução |
Exercícios
de Consolidação A + BC + (Utilizando portas de 3 entradas e
utilizando portas de apenas 2 entradas) A. A + BC . A + B+C .
|
NAND |
AB + A+B + |
|
|
|
|
|
|
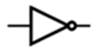
NOT
|
|
||||||||||
|
A+ |
A+B+ (No logisim resolve
o exercício utilizando portas de 3 entradas e utilizando portas de apenas 2 entradas) |
NOR |
e A+B . A.B . |
XOR OU Exclusiva A.B
XNOR OU Coincidencia |
Xor XNOR |
|
||||||
|
|
Porta OR
|
A+B+C |
||||||||||
|
|
|
|
- Portas com 3 e 2 entradas - Desenhar no papel - Tabela de verdade |
|
|
|
|
|||||
Caso seja necessário: Como abrir a
resolução dos exercícios no Windows 10
|
http://www.mathematik.uni-marburg.de/~thormae/lectures/ti1/code/karnaughmap/ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Extrair expressões Booleanas de
tabelas de verdade. Há duas formas de se definir (ou descrever) uma função Booleana: 1º Descrevendo-se todas as situações das variáveis de entrada para as
quais a função vale 1. Este método é conhecido por soma de produtos (SdP), Sum of Product (SOP) 2º Descrevendo-se todas as situações das variáveis de entrada para as
quais a função vale 0. Este método é conhecido por produto de somas (PdS). Product of Sums (POS) Extrair expressões Booleanas de circuitos lógicos. Simplificar expressões pelo método de karnaugh (2 entradas). Regra da adjacência - De uma coluna para outra apenas uma variável pode mudar de estado. Enlace – Apenas podemos enlaçar 2, 4, 8, 16…. Uns. Simplificar
expressões pelo método álgebra booleana |
Tabela de verdade para expressão Desafio9.1TabToExp & Resolvido |
Simplificação
de expressões a 2 variáveis Mapa de karnaugh Simplificação
de expressões a 3 variáveis Mapa de karnaugh |
Comprovação das propriedades: comutativa,
associativa e distributiva. Comprovação da regra de precedência das operações lógicas DesafioBPropriedades + Resolvido Comprovação das Identidades auxiliares 15_16_17_DessafioIdentidades Comprovação dos teoremas de De Morgan 18e19DeMorgan + Ajuda + Resolvido |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Circuito lógico para expressão Desafio10CircToExp & Resolvido Desafio10.1CircToExp & Resolvido |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Tabela de verdade para … |
||||||||||
|
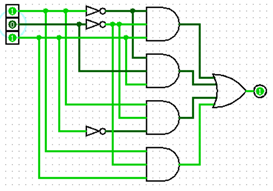
Tendo em conta a expressão X Ver Exemplo a) Calcular o nº de saídas possíveis b) Desenhar o circuito no logisim c) Desenhar o diagrama temporal d) Preencher a tabela de
verdade e) Conclusão |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Circuito para… |
||||||||||
|
Tendo em conta a expressão X Ver Exemplo a) Calcular o nº de saídas possíveis b) Desenhar o circuito no logisim c) Desenhar o diagrama temporal d) Preencher a tabela de verdade e) Conclusão |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A.B. (UTILIZANDO PORTAS DE 3 ENTRADAS E
UTILIZANDO PORTAS DE APENAS 2 ENTRADAS) |
|
Porta Lógica - Logic Gate AND ou E ou * Porta NOT ou INVERTER (inversor) |
|
|
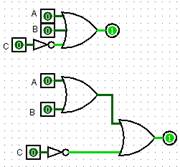
Desafio2.2OrNot (No logisim
resolve o exercício utilizando portas de 3 entradas e utilizando portas de
apenas 2 entradas) |
|
Porta Lógica - Logic Gate OR ou OU ou
+ Porta NOT ou INVERTER (inversor) |
|
|
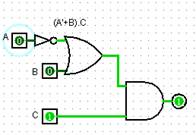
(A+B).C |
|
Porta Lógica - Logic Gate AND ou E ou * Porta Lógica - Logic Gate OR ou OU ou + |
|
|
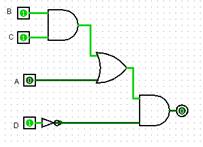
(A.B)+C |
|
Porta Lógica - Logic Gate AND ou E ou * Porta Lógica - Logic Gate OR ou OU ou + |
|
|
( |
|
Porta Lógica - Logic Gate AND ou E ou * Porta Lógica - Logic Gate OR ou OU ou + Porta NOT ou INVERTER (inversor) |
|
|
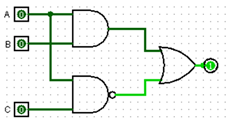
A + BC . |
|
|
|
|
|
|
Porta Lógica - Logic Gate AND ou E ou * Porta Lógica - Logic Gate OR ou OU ou + Porta Lógica - Logic Gate NAND (Não E) |
|
|
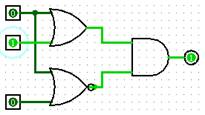
A+B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Desafio11Kmap |
|
|
|
|
Desafio11.3Kmap |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
Teoremas da álgebra de Boole |
||||
|
Soma |
|
Produto |
||
|
A+0=A |
0+0=0 |
|
A.0=0 |
0.0=0 |
|
1+0=1 |
1.0=0 |
|||
|
A+1=1 |
0+1=1 |
A.1=A |
0.1=0 |
|
|
1+1=1 |
1.1=1 |
|||
|
A+A=A |
0+0=0 1+1=1 |
A.A=A |
0.0=0 1.1=1 |
|
|
A+A’=1 |
1+0=1 |
A.A’=0 |
1.0=0 |
|
|
0+1=1 |
0.1=0 |
|||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Porta NOT ou INVERTER (inversor) Desafio
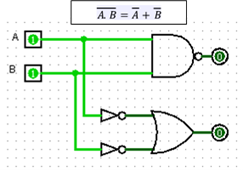
1.1 – Tendo em conta a expressão A .
b) Preencher a tabela de verdade. c) Desenhar o circuito no logisim. d) Desenhar o diagrama temporal. e) Conclusão. Resolução a) Calcular o nº de saídas possíveis. Resposta 22=4 b) Preencher a tabela de verdade
b) Desenhar o circuito no logisim. c) Desenhar o diagrama temporal.
f) Conclusão. A saída (s) só será
1 quando A=1 e B=0. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||